🎓渲染管线(Pipeline)

type
status
date
slug
summary
tags
category
icon
password
😀
最近学习的过程平缓，每天都在稳稳进步。放慢脚步，写写博客，输出一些内容也利于消化。
 

渲染管线

顾名思义，渲染管线也就是我们常说的 The Graphics Pipeline，定义由图形数据到渲染结束的整个过程。
渲染管线
渲染管线
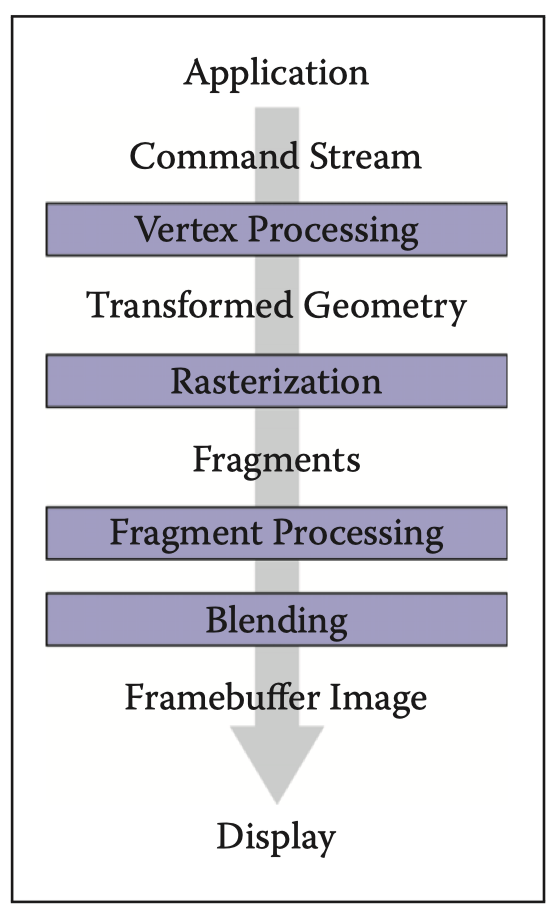
在虎书中定义的渲染管线如图所示，其定义的是在图形渲染中的泛流程，而不是具体某个渲染引擎（如OpenGL）。
现在大多使用的渲染按对象顺序渲染，而不是像素顺序渲染，这点作为前置知识非常重要。

Vertex Processing 顶点处理

在这一阶段，我们需要对顶点进行变换，将其映射到屏幕空间当中，并预处理一些后续流程中需要用到的数据。

MV 变换

首先需要进行：
  1. Model 变换，将模型坐标转化为世界坐标。
  1. View 变换，将相机放置到标准位置，并且对世界空间进行变换。
经过这两次变换，我们得到标准的世界空间坐标（将相机放置在原点）。

Clip 截断

在进行投影变换之前，我们需要对视锥（体）外的物体进行一些截断。
为什么需要这一步？
答案是，透视投影会对坐标的深度（z）产生非线性的扭曲。
这会导致一些在视锥体外的图元被非正常的渲染，特别是在 near 平面之外的部分。
透视投影 & 非线性扭曲的深度
透视投影 & 非线性扭曲的深度
 
如图所示，三角形abc，经过投影得到a’b’c’,由于透视投影会对z进行非线性的扭曲，导致 near 后的顶点 c 经过变换后，c’ 反而位于 near 平面之前。
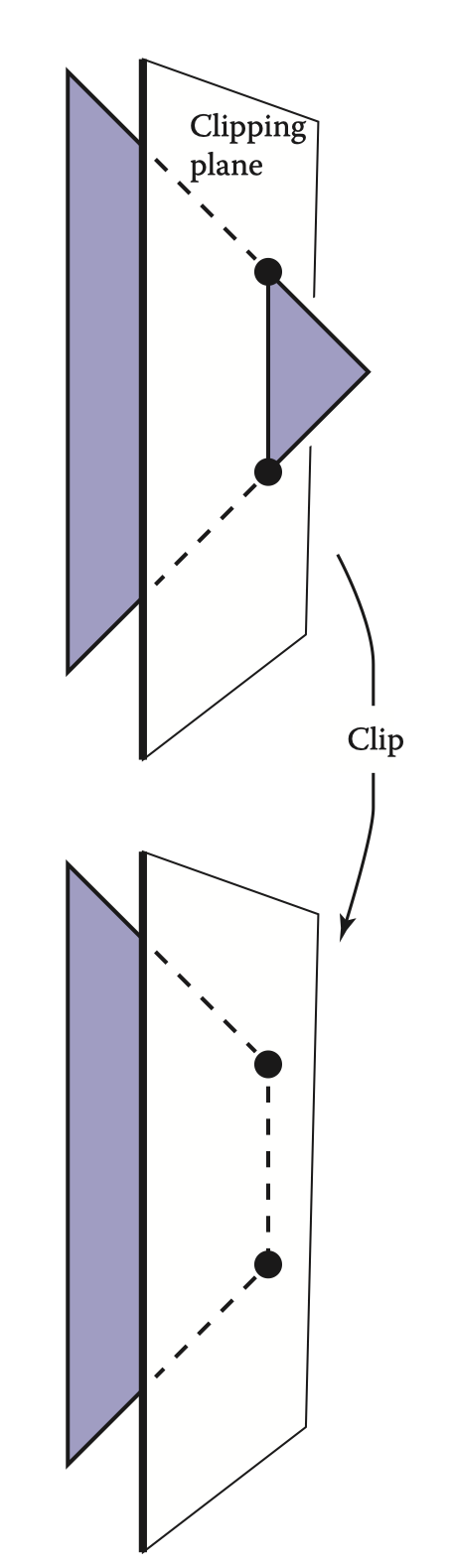
因此，我们通常对 near 平面进行截断，例如将三角形截断成类梯形，保证在经过透视投影后，能够保证图元正常被渲染。
类似的截断操作如右图所示，在图元的操作等级中，直接改变图元的形状。
 
notion image
在计算机图形学中，图元（Primitive） 是构建图形的基本元素。常见的图元包括：
  • 点（Point）：最简单的图元，用于表示单个位置。
  • 线段（Line）：由两个点定义的直线。
  • 三角形（Triangle）：由三个顶点定义的多边形，是最常用的图元，因为任何复杂的形状都可以通过三角形来逼近

PV 变化

在裁剪完成之后，我们可以进行投影变换：
  • 正交投影，保持物体的大小信息
  • 透视投影，模拟真实世界中近大远小的特点
在投影变换完成之后，我们得到一个处在 的标准视体。
接着，我们对这个视体进行 Viewport 视口变化，将其变换到屏幕的坐标系当中（通常左下角为起点）。
当然，这些变换矩阵都可以相乘为同一个矩阵，作为核函数传递给GPU，进行大规模的并行运算。

Rasterization 光栅化

顶点处理完成之后，我们已经获得屏幕坐标下的物体集合及其计算所需要的数据。
这些数据大致包括：
  • 坐标信息，通常是(x,y,z)，虽然深度信息在投影中不需要，但是保留其大小关系很重要。
  • 法线信息，用于后续的Shading流程。
  • 图元的其他信息，如颜色，透明度等。
光栅化的过程是将顶点信息计算为逐像素的片元信息（Fragment）。

直线

直线的光栅化比较简单，分为两个步骤：
  1. 通过斜率，观察 x 和 y 的变换速度
      2. 比如对于斜率处于(0,1)之间的直线，x 的变换速率更快。
  1. 枚举变换快的坐标轴，枚举并渲染。
      2. 以x距离，枚举 x，根据中点来判断下次选择哪一个像素。 比如，对于点(x,y)，下一个点在
    1. (x + 1, y + 1)
    2. (x + 1, y)
      3. 中选取，选取的逻辑是判断两者的中点(x + 1, y + 0.5)在直线的上方还是下方。
这样保证在变换快的坐标轴上不发生跳变，保持连续。
当然，这个过程也可以使用增量式的计算，来减小计算量，我在这里也仅是粗略的了解和介绍，感兴趣的读者可以自行查阅虎书的对应章节。

三角形

三角形的光栅化也分为两个步骤：
  1. 渲染三角形内的点
  1. 渲染三角形边上的点
为何要将三角形内的点与边上的点分来作渲染？
因为多面体通常由三角形拼接而成，为保证相邻三角形不会由空洞（hole），因此对共享边只进行一次渲染操作。
如何判定点是否在三角形当中？
通常可以使用向量叉乘法，如果三个叉乘结果同号则说明在三边的同一侧（注意边长的顺序要首尾衔接）。
但是由于后续需要用到属性的插值（interpolate），因此我们将点 P 的坐标转换为重心坐标系下的坐标，即
只要三个坐标值都大于零，且和为1，则说明在三角形内部。
具体的计算公式这里直接给出，可以通过向量进行证明，这里不再赘述。
其中，三边的直线方程可以表示为：
属性插值
对于一些顶点属性，我们可以采用重心坐标直接进行属性插值，我们以颜色（Color）举例，对于三角形内的任意一点 而言：
同理，对于一些其他的属性（如法线、深度）都可以使用重心坐标进行插值。
性能提升
我们当然不需要针对单一三角形图元，遍历整个屏幕的所有像素，优点方向有：
  • 我们可以使用 bounding box，用一个矩形框住三角形，减少计算量。
  • 涉及到直线计算，理所当然的可以使用增量计算。

Hidden Surface Removal

在计算片元信息的时候，我们当然需要隐藏被遮挡的平面（或者说处理遮挡信息，如果有透明度的话）。
画家算法
画家算法是一种古老的算法，简单的将后渲染（后画）的物体的像素值进行覆盖，这样做有两个大的弊端：
  1. 计算“渲染顺序”通常是一件逻辑上及其复杂，且计算复杂度高的任务，对性能和程序员都不友好。
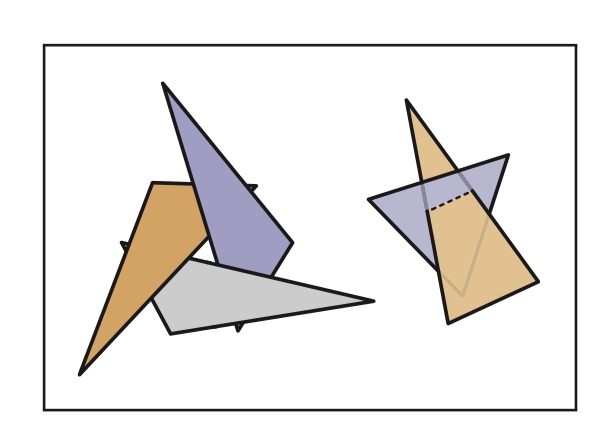
  1. 有些对象之间没有明显的顺序可言，如下图的相交三角形。
      2. notion image
Z-Buffer
目前，更受欢迎的算法是Z-buffer，该算法简单且高效。
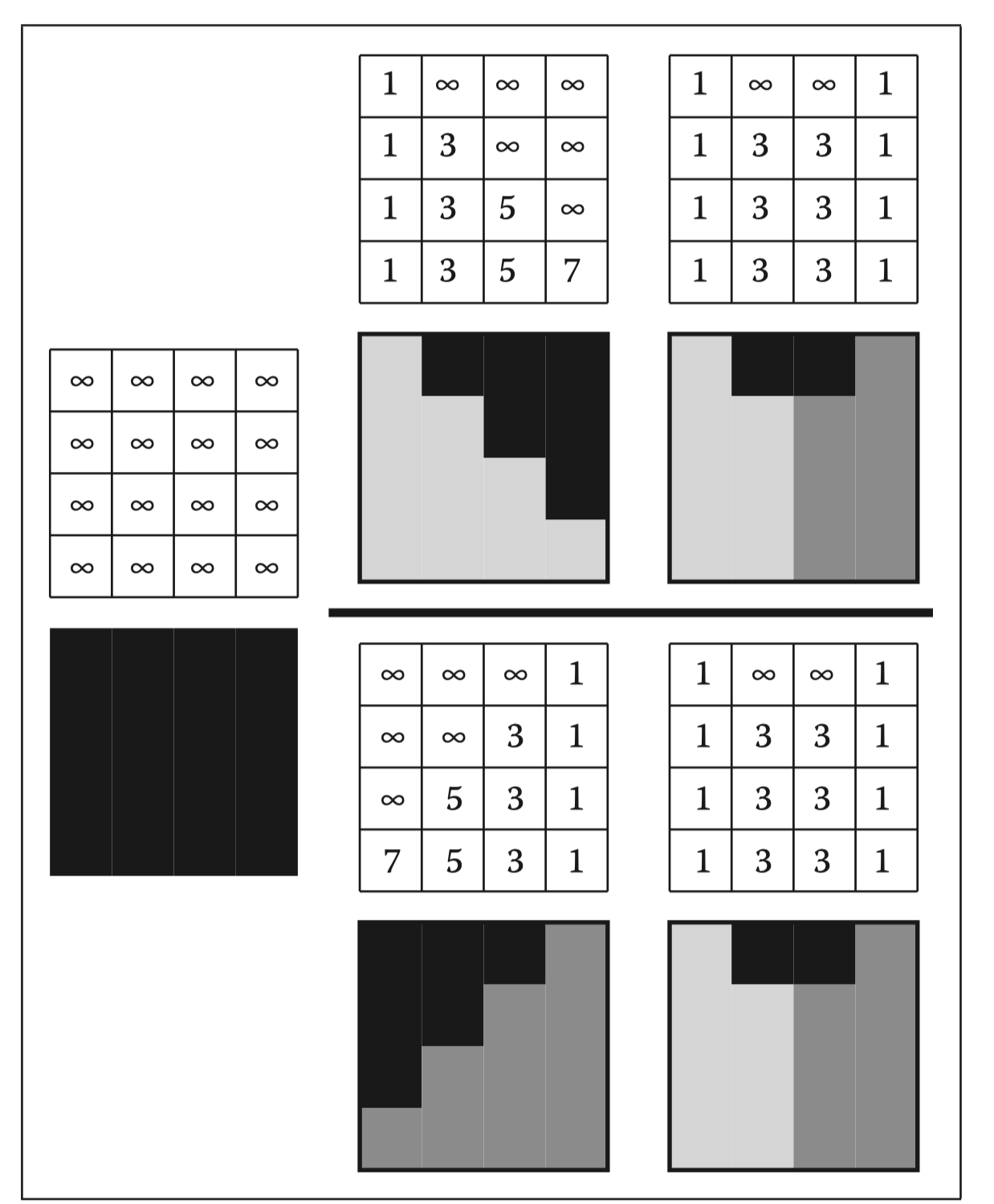
该算法的主要思路是将每个像素的FrameBuffer新增一个维度，叫做Z-Buffer（深度缓冲），记录这个像素中最近的物体的距离。
回忆在View变换章节当中，我们提到，透视投影虽然会非线性的扭曲深度，但是会保留相对的大小顺序。
在计算一个像素的片元时，如果该像素的深度小于Z-buffer中的数值，则更新Z-buffer，并更新（计算）片元信息。
初始时，将所有的Z-buffer初始化为最大值，保证渲染结果与顺序无关。
Z-Buffer
Z-Buffer

总结

在光栅化阶段结束后，我们应该得到屏幕当中每个像素的片元信息。
⚠️
不要忘记渲染顺序，object order。

Fragment Process

在光栅化结束之后，我们需要对片元进行进一步的处理。
而主要的处理过程分为：
  1. Shading - 与光照结合，计算像素的真实颜色。
  1. Texture Mapping - 纹理映射，使物体更加真实。
在光栅化的过程中，我们已经完成了对基本颜色、属性的插值，但这样生成的图像属性均匀变化，失真严重。
因此，需要结合光照，进一步得到图像更真实的颜色。

Per-Vertex Shading

很直观的，因为法线信息一般存储在顶点上，我们可以在顶点位置上进行Shading（着色）。
对于每个顶点，我们通过一些光学模型的计算，得到真实的像素颜色值。
中间像素的处理
对于平面中的某个非顶点的像素，我们通过与光栅化过程类似的属性插值，得到中间像素的颜色。
不足之处
考虑对房间地板着色的情景：
  1. 该地板由两个大的三角形图元拼接而成
  1. 光源处于房间的正中间位置。
在Per-Vertex Shading当中，中间地板的颜色通过对顶点着色颜色的插值而得到，我们会发现地板的中间部分过于暗，失真严重。
逐顶点着色
逐顶点着色

Per-fragment Shading

显然，只在顶点上计算光照shading是不够的。
因此，我们考虑对每个片元进行着色。
那么就有一个问题：
如何得到法线信息？
在光照模型的计算当中，我们需要该着色点的法线信息，而这些信息只存在与顶点当中。
因此，我们选择对顶点提供的法线进行插值计算，得到图元中逐片元的法线信息。
而这一步插值，需要在顶点处理或光栅化过程中完成。
有了像素的法线信息，我们直接进行光线模型的计算，就可以得到该像素的颜色。
可能很多人会有一些疑惑，
对着色后的颜色进行插值，与对法线进行插值有什么区别？
答案是计算不同。
  • 在顶点着色过程当中，我们仅仅顶点进行光照模型计算，而其他像素的颜色由插值得到。
  • 在片元着色过程当中，我们对每个片元（或者说像素）都进行了光照模型计算，由顶点插值得到可用的法线。
因此，总的来讲，顶点着色的计算量更少，而片元着色的效果更好。
逐片元着色
逐片元着色

Texture Mapping

在逐片元着色当中，我们提到，光线模型的计算需要法线信息。
而我们直观的策略是通过插值得到中间片元的法线，但之前的问题依然存在：
插值得到的法线过于平均，失真比较强。
因此，我们可以通过 Texture Mapping 来解决这个问题。
对于每个片元，我们提供一个可供映射的法线（或者其他属性），弃用法线插值。
这就是 Texture Mapping 的过程。

Blend

混合后，将计算好 FrameBuffer 送给显卡进行渲染。
这个过程虎书当中也没有特殊解释，只是说有这个阶段而已，感兴趣的读者可以自行学习。

📎 参考文章

  • 虎书
  • 《Games 101》
 
上一篇
GAMES101 作业3
下一篇
View(MVPV)变换
Loading...
文章列表
目录